Introducción al área de polígonos irregulares para niños
Como Calcular El Area De Un Poligono Irregular Para Niños – ¡Hola, pequeños exploradores matemáticos! Vamos a descubrir un mundo fascinante: ¡el área de los polígonos irregulares! Imaginen que el área es como la cantidad de espacio que ocupa una figura en una superficie. Piensen en un rompecabezas: cada pieza tiene su propio espacio, su propia área. Los polígonos irregulares son como piezas de rompecabezas un poco… ¡diferentes! No son tan ordenados como los cuadrados o los rectángulos.
¡Pero eso no significa que sean menos interesantes!El área de un polígono irregular, al igual que la de uno regular, se mide en unidades cuadradas, como centímetros cuadrados (cm²) o metros cuadrados (m²). Es como contar cuántos cuadraditos caben dentro de la figura. Para polígonos irregulares, este conteo directo puede ser un poco complicado, ¡pero hay trucos geniales que veremos más adelante!
Tipos de polígonos irregulares
Los polígonos irregulares son figuras geométricas cerradas con lados de diferentes longitudes y ángulos que no son iguales. A diferencia de los polígonos regulares (como el cuadrado o el triángulo equilátero), sus lados y ángulos no son todos iguales. ¡Hay una gran variedad de ellos! Algunos ejemplos incluyen pentágonos irregulares (5 lados), hexágonos irregulares (6 lados), heptágonos irregulares (7 lados), y muchos más.
La imaginación es el límite!
| Polígono Irregular | Nombre | Descripción | Ejemplo Visual (Descripción) |
|---|---|---|---|
| Una figura con 5 lados de diferentes longitudes y ángulos | Pentágono Irregular | Piensa en una estrella de mar, ¡sus puntas no son todas iguales! | Imaginen una estrella de mar con brazos de diferentes longitudes. Uno puede ser más largo, otro más corto, y los ángulos entre los brazos son desiguales. |
| Una figura con 6 lados de diferentes longitudes y ángulos | Hexágono Irregular | Como un panal de abejas un poco… ¡desordenado! | Visualicen un panal de abejas donde algunas celdas son más grandes o más pequeñas que otras, y los ángulos entre las celdas no son todos iguales. |
| Una figura con 7 lados de diferentes longitudes y ángulos | Heptágono Irregular | Una piedra con siete lados desiguales. | Imaginen una piedra recolectada en la playa. Tiene siete lados de longitudes y ángulos variables, algunos lados son curvos, otros rectos. |
| Una figura con muchos lados de diferentes longitudes y ángulos | Polígono Irregular Complejo | Una forma irregular con muchos lados y ángulos, como la silueta de una hoja. | Piensen en la silueta de una hoja. Tiene muchos lados curvos y rectos, y no hay dos lados iguales ni ángulos iguales. |
Actividad: ¡Caza de Polígonos Irregulares!
¡Es hora de poner en práctica lo aprendido! Salgan a explorar su casa, su jardín o el parque cercano. Busquen objetos que tengan forma de polígonos irregulares. Puede ser una hoja, una piedra, una galleta, ¡o cualquier cosa que se les ocurra! Dibujen lo que encuentren y traten de identificar cuántos lados tiene cada figura. ¡Será una divertida aventura matemática! Anoten el nombre del objeto y cuántos lados tiene su forma irregular.
Este ejercicio les ayudará a comprender mejor cómo se ven los polígonos irregulares en el mundo real.
Métodos para calcular el área de un polígono irregular
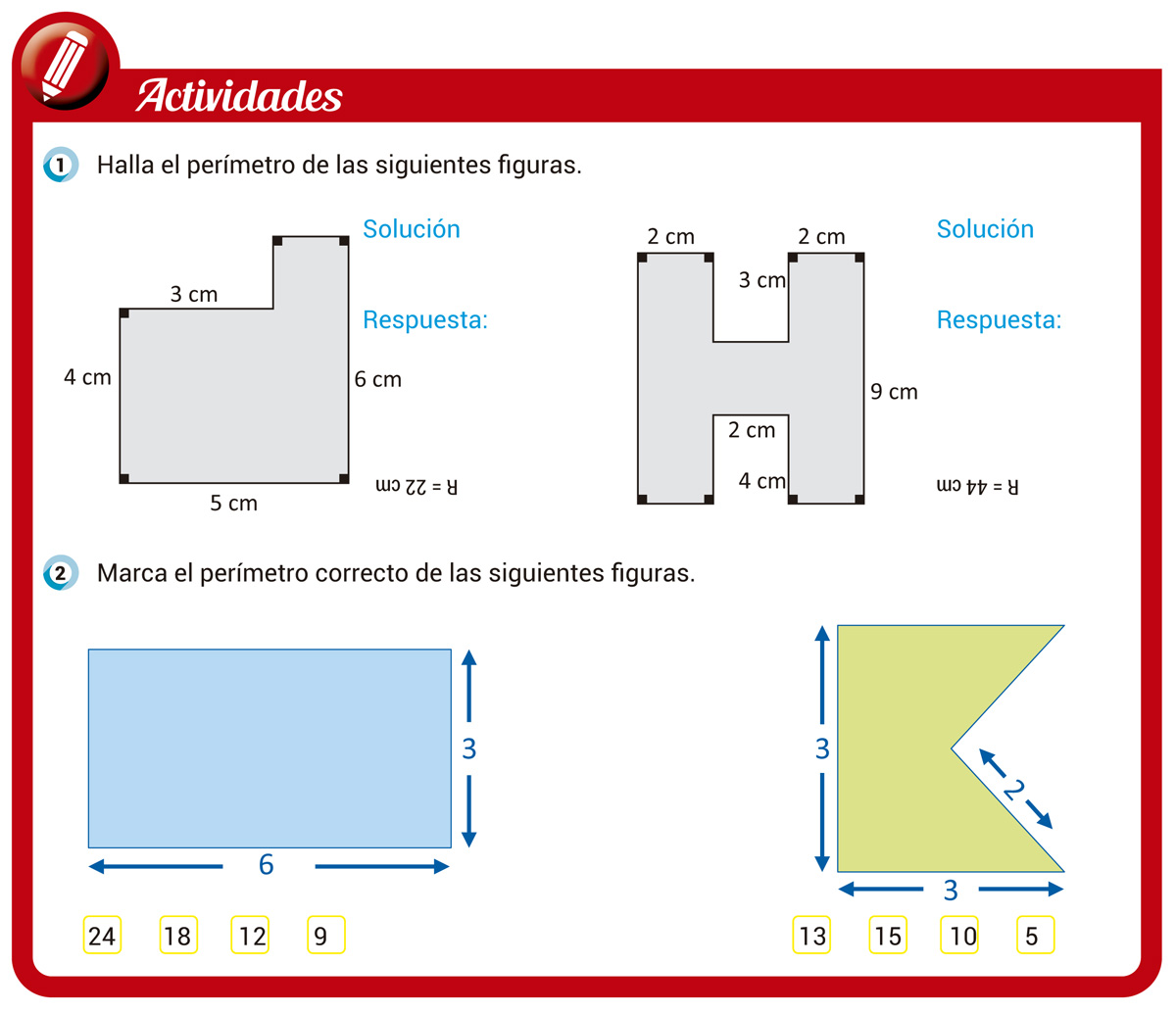
¡Calcular el área de un polígono irregular puede parecer un desafío, pero con los métodos adecuados, ¡es pan comido! Vamos a explorar dos maneras geniales de hacerlo: descomponiéndolo en figuras regulares y usando una cuadrícula. Prepárate para convertirte en un experto en áreas.
Descomposición en Figuras Regulares
Este método es como un rompecabezas geométrico. La idea es dividir el polígono irregular en varias figuras geométricas regulares, como triángulos y rectángulos, cuyas áreas sabemos calcular fácilmente. Una vez que tenemos esas áreas individuales, ¡simplemente las sumamos! Es como construir un castillo con bloques: cada bloque es una figura regular, y el castillo completo es nuestro polígono irregular.Imaginemos un polígono irregular que se asemeja a una casa con un tejado puntiagudo.
Podemos dividirlo en un rectángulo (la casa) y dos triángulos (el tejado). Para calcular el área del rectángulo, necesitamos su base y su altura. Supongamos que la base mide 6 cm y la altura 4 cm. El área del rectángulo sería 6 cm
4 cm = 24 cm².
Ahora, para los triángulos. Necesitamos la base y la altura de cada uno. Supongamos que cada triángulo tiene una base de 3 cm y una altura de 2 cm. El área de un triángulo se calcula como (base
- altura) / 2. En este caso, el área de cada triángulo sería (3 cm
- 2 cm) / 2 = 3 cm². Como tenemos dos triángulos, el área total de los triángulos es 3 cm² + 3 cm² = 6 cm².
Finalmente, sumamos el área del rectángulo y la de los dos triángulos: 24 cm² + 6 cm² = 30 cm². ¡Listo! El área del polígono irregular es de 30 cm². Piensa en ello como sumar las piezas de un rompecabezas para obtener la imagen completa. Recuerda que la precisión depende de la exactitud de las medidas de las figuras regulares.
Método de la Cuadrícula
Este método es perfecto para una estimación rápida. Dibuja una cuadrícula sobre el polígono irregular. Cada cuadrado de la cuadrícula representa una unidad de área. Cuenta los cuadrados que están completamente dentro del polígono. Luego, estima el área de los cuadrados que están parcialmente dentro del polígono.
Puedes dividir los cuadrados parcialmente cubiertos a la mitad o en cuartos, dependiendo de la proporción que esté dentro del polígono. Suma el número de cuadrados completos y las estimaciones de los cuadrados parciales para obtener una aproximación del área total. Este método es ideal cuando no se necesita mucha precisión, como para estimar la superficie de un lago irregular en un mapa.
Fórmula de Herón para el Área de un Triángulo
La fórmula de Herón es una herramienta poderosa para calcular el área de un triángulo cuando conocemos la longitud de sus tres lados. Es especialmente útil cuando no conocemos la altura del triángulo. La fórmula es:
Área = √[s(s-a)(s-b)(s-c)]
donde:* a, b, y c son las longitudes de los lados del triángulo.
s es el semiperímetro del triángulo, calculado como s = (a + b + c) / 2.
Por ejemplo, si un triángulo tiene lados de 5 cm, 6 cm y 7 cm, el semiperímetro sería s = (5 + 6 + 7) / 2 = 9 cm. Aplicando la fórmula de Herón:Área = √[9(9-5)(9-6)(9-7)] = √[9
- 4
- 3
- 2] = √216 ≈ 14.7 cm²
Comparación de Métodos, Como Calcular El Area De Un Poligono Irregular Para Niños
| Método | Descripción |
|---|---|
| Descomposición en Figuras Regulares | Divide el polígono en figuras regulares (triángulos, rectángulos, etc.) y suma sus áreas. Proporciona resultados precisos si las medidas son exactas. |
| Método de la Cuadrícula | Estima el área contando cuadrados en una cuadrícula sobre el polígono. Es rápido y sencillo, pero menos preciso que el método de descomposición. |
Ejemplos y ejercicios prácticos: Como Calcular El Area De Un Poligono Irregular Para Niños
¡Ahora sí, manos a la obra! Vamos a practicar el cálculo del área de polígonos irregulares con algunos ejemplos. Verás que, aunque parezcan complicados al principio, con un poco de práctica se vuelven pan comido. Recuerda que la clave está en dividir la figura en formas más sencillas, como rectángulos y triángulos, ¡y luego sumar sus áreas!A continuación, te presentamos tres ejemplos con diferentes niveles de dificultad, para que puedas ir poco a poco y dominar la técnica.
Cada paso está explicado detalladamente para que no te pierdas.
Ejemplo 1: Polígono Irregular Simple
Imagina un polígono irregular que se asemeja a una casa con un tejado inclinado. Este polígono se puede dividir fácilmente en un rectángulo y un triángulo. Supongamos que el rectángulo tiene una base de 6 cm y una altura de 4 cm. El triángulo que forma el techo tiene una base de 6 cm y una altura de 3 cm.
- Paso 1: Calcular el área del rectángulo. La fórmula es base x altura. Entonces, el área del rectángulo es 6 cm x 4 cm = 24 cm².
- Paso 2: Calcular el área del triángulo. La fórmula es (base x altura) / 2. El área del triángulo es (6 cm x 3 cm) / 2 = 9 cm².
- Paso 3: Sumar las áreas. Para obtener el área total del polígono irregular, sumamos las áreas del rectángulo y el triángulo: 24 cm² + 9 cm² = 33 cm².
Ejemplo 2: Polígono Irregular de Mayor Complejidad
Ahora, vamos a intentar con un polígono un poco más complicado. Piensa en una figura que se parece a un trapecio irregular. Podemos dividirlo en un rectángulo y dos triángulos. Supongamos que el rectángulo tiene una base de 5 cm y una altura de 4 cm. Los dos triángulos tienen bases de 2 cm y 3 cm respectivamente, y ambos tienen una altura de 2 cm.
- Paso 1: Área del rectángulo: 5 cm x 4 cm = 20 cm²
- Paso 2: Área del triángulo 1: (2 cm x 2 cm) / 2 = 2 cm²
- Paso 3: Área del triángulo 2: (3 cm x 2 cm) / 2 = 3 cm²
- Paso 4: Área total: 20 cm² + 2 cm² + 3 cm² = 25 cm²
Ejemplo 3: Polígono Irregular con División en Más Figuras
Este ejemplo es el más desafiante. Imaginemos un polígono irregular que se asemeja a una hoja irregular. Para calcular su área, lo dividimos en un cuadrado, un rectángulo y dos triángulos. El cuadrado tiene lados de 3 cm. El rectángulo tiene una base de 4 cm y una altura de 2 cm.
Los dos triángulos tienen una base de 3 cm y una altura de 2 cm cada uno.
- Paso 1: Área del cuadrado: 3 cm x 3 cm = 9 cm²
- Paso 2: Área del rectángulo: 4 cm x 2 cm = 8 cm²
- Paso 3: Área de cada triángulo: (3 cm x 2 cm) / 2 = 3 cm² (x2 triángulos = 6 cm²)
- Paso 4: Área total: 9 cm² + 8 cm² + 6 cm² = 23 cm²
Ejercicio Práctico: El Jardín de María
María quiere plantar flores en su jardín, que tiene una forma irregular. El jardín se puede representar como un polígono con los siguientes vértices: A(0,0), B(4,0), C(6,2), D(5,4), E(2,4), F(0,2). Dibuja el polígono en una cuadrícula y calcula su área. Recuerda que puedes dividirlo en figuras geométricas más simples para facilitar el cálculo. ¡Inténtalo! Recuerda que cada cuadro de la cuadrícula representa 1 cm².
Ejercicios de Medición y Cálculo
Para afianzar tus conocimientos, te proponemos una serie de ejercicios donde deberás medir las longitudes de los lados de diferentes polígonos irregulares y, utilizando los métodos aprendidos, calcular sus áreas. Recuerda utilizar una regla para obtener las medidas con precisión. Puedes dibujar tus propios polígonos irregulares o utilizar recortes de papel con formas irregulares. ¡A medir y calcular!
